Las maquinas automáticas que lanzan pelotas de béisbol, se pueden ajustar para variar la trayectoria del lanzamiento. Si dos pelotas llegan al mismo blanco, pero en trayectoria diferentes, ¿cuál de ellas llega en menos tiempo?
La respuesta, la publicaremos el sig. lunes y mencionaremos a quien deje el mejor comentario al respecto.
Respuesta: El tiempo de vuelo equivale a las coordenadas x = 0 y = 0 de modo que el tiempo neto es:
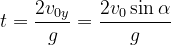
Si la velocidad es la misma para los dos tiros, el de menor ángulo tarda menos tiempo en el aire.
Felicidades a todos por sus comentarios, especialmente a Belen, opium, borjage, y a lez.
Respuesta: El tiempo de vuelo equivale a las coordenadas x = 0 y = 0 de modo que el tiempo neto es:
Si la velocidad es la misma para los dos tiros, el de menor ángulo tarda menos tiempo en el aire.
Felicidades a todos por sus comentarios, especialmente a Belen, opium, borjage, y a lez.
Aquel cuyo ángulo de tiro parabólico sea menor.
ResponderBorrarEsto se ve porque el alcance es proporcional a sin(alpha), que es creciente entre 0 y 2Pi, mientras que el alcance es proporcional a sin(2*alpha), que es simétrica con respecto a Pi/4, con lo cual hay dos alcances iguales, pero el tiempo entre 0 y 2pi es estrictamente creciente.
R = v^2 * sin(2*alpha) / g
t = 2*v*sin(alpha)/g
También se puede ver de otra manera. Hay dos alphas a las que se puede dar un alcance dado. A menor alpha, mayor v_x tenemos, y por lo tanto, llegamos en menos tiempo llegamos a cualquier parte desde el punto de vista horizontal.
Saludos
LLegan al mismo yiempo porque en un tiro oblicuo el dezplazamiento horizontal es a velocidad constante a diferencia del vertical que es acelerado
ResponderBorrarla trayectoria que une dos puntos siempre es la gradiente de la función que la define, ya que éste ubique la dirección de mayor variación. en el caso del tiro parabolico puro más sencillo el gradiente es <2x,0,0> de modo que la trayectoria que más se acerque a una línea recta es la que llegara antes.
ResponderBorrarme comi una palabra. la menor trayectoria es la gradiente.
ResponderBorrarEs fácil. Aquella cuya trayectoria sea más corta.
ResponderBorrarSuponiendo que están inicialmente a la misma distancia del blanco llegará en menos tiempo la que tenga un menor ángulo de salida.
No es acaso este el problema de la Braquistócrona?
ResponderBorrarLa solución es la cicloide. Esto se hace con calculo de variaciones. Es un problema histórico interesante, planteado por Johann Bernoulli y resuelto por Newton anónimamente.
La cicloide es la curva que describe un punto de una circunferencia que rueda sobre una recta sin deslizar. La ciclode se pude dibujar si colocamos un marcador en la periferia de un aro, hacemos rodar éste, sin deslizar, de manera que el marcador marque en una superficie su movimiento, el marcador trazará una cicloide con su parte cóncava hacia abajo. Si este dibujo se da vuelta, obtendrá una braquistocrona. Aunque no se si una máquina puede provocar el efecto para que un objeto recorra esta curva
Llegará en menos tiempo aquella que describa una elípse (ya que el tiro parabólico es sólo una aproximación útil sólo a efectos prácticos, pero realmente todos los tiros son elípticos)con una excentricidad mayor. Es decir, llegará en menos tiempo aquella bola que gane menos altura.
ResponderBorrarTango Alfa.
Algo me dice que el tiempo es el mismo....nose, será mi intuición de físico jajaja
ResponderBorrarMejorar enunciado,
ResponderBorraratte
neromero
Cuando uno resuelve un problema de tiro parabólico, básicamente lo que se hace es "simplificar" un problema de 2 dimensiones, en 2 problemas unidimensionales interelacionados entre sí. La condición de nuestro problema, es que ambas trayectorias tengan los mismos puntos finales, digamos que la pelota habrá recorido una disttancia L y se encontrará a ras de suelo, entonces nuestras posiciones finales serán: x=L,y=0 Para saber cual de los dos movimientos es más rapido, deberemos descomponer la velocidad en 2 componentes (vertical y horizontal). Tenemos pues que a angulos pequeños, tenemos una velocidad en x grande y en y pequeña y el caso opuesto para angulos grandes. Si queremos que nuestra pelota permanezca el menor tiempo posible en el aire debera tener una velocidad y pequeña y si queremos que recorra una distancia x lo mas rapido posible, querremos que la velocidad en x sea lo mas rapido posible, por tanto, la bola alnzada con ángulo menor, siempre será la que menos tardará.
ResponderBorrarpor un momento pensé que el tiempo seria igual, pero la realidad es que no.
ResponderBorrarel tiro parabólico se divide en dos partes. una vertical y otra horizontal :
Vx & Vy
aunque las velocidades Vx de ambas pelotas sean iguales la velocidad Vy no lo es, por lo tanto una tarda mas tiempo en llegar al punto que otra. la que recorre en menor tiempo la distancia es la que tiene un angulo menor de salida.
llega primero el que tiene como trayectoria el tiro horizontal aunque la velocidad es igual una tarda mas tiempo que la otra en llegar al punto final porque la que tiene mayor angulo es la que tarda mas por el tiro vertical que hace en su recorrido
ResponderBorrarHola!
ResponderBorrarAlguien tiene a mano, o sabe si existe algún modelo o ecuación empírica para el tiro parabólico real: con rozamiento del aire, teniendo en cuenta el coeficiente de arrastre del objeto lanzado y su sección eficaz, la densidad del aire, distribución de velocidades de viento atravesadas, etc.
Por ej: un globo de agua de 1000 litros lanzado para llegar idealmente a 10 kilómetros. ¿Cuál será la posición y el tiempo de llegada en un plano?
Muchas gracias!