5 ejemplos sencillos sobre la correlación y ajuste de líneas, con Excel.

Todos los que nos dedicamos a presentar información por medio de gráficos debemos dominiar el ajuste de curvas a una serie de datos, este post es un comentario sobre la relación de la correlación a los ajustes de líneas rectas.

Cuando hacemos un experimento lo mejor es sólo variar una variable y observar una sola respuesta a ese estimulo. Después, debemos presentar esos datos en un gráfico y buscar una ecuación matemática que nos permita extraer la información de comportamiento que observamos y predecir otros casos.

Pues bien, para mostrar la relación entre la correlación de datos experimentales (que aquí llamamos R cuadrada) y los puntos obtenidos por un ajuste de datos (como es el método de mínimos cuadrados), les presento 5 ejemplos básicos de cómo funciona.

Por ser muy popular, emplee Excel para hacer los gráficos y simulaciones numéricas. 

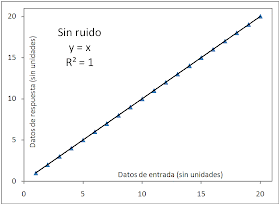Caso 1. En una columna hice una serie de números que varían linealmente 1:1:20, y los grafique contra su clon. Por medio de botones alternos, Excel puede desplegar líneas de tendencia, la ecuación de ajuste y el factor R^2 para que se muestre en el gráfico. En este y los otros casos escogimos un ajuste lineal pues este es un ejemplo introductorio y porque la regresión lineal es el modelo matemático muy fácil de interpretar desde el punto de vista físico.

El resultado es una línea que empata con todos los puntos experimentales (que nosotros creamos ;) ), por lo cual el factor R^2 es 1. R^2 es un índice normalizado, de intervalo de 1 a 0, el 1 significa que nuestra elección de ajuste es adecuado, mientras que el 0 representa un pésimo ajuste. Como veremos en este post, es cuestión de criterio que ajuste emplear.

Caso 2. A cada uno de los datos de respuesta originales les he sumando un número aleatorio, use una función propia de Excel que genera los números aleatorios entre 0 y 1. Al obtener la línea de tendencia, observamos que no todos los puntos empatan en los puntos, eso era lo que esperábamos. Por lo cual, efectivamente el factor R^2 disminuyo hasta 0.9981, lo que significa que es una alta correlación, por lo cual el ajuste sigue siendo adecuado pese al ruido presente.

Caso 3. Ahora aumente el nivel de ruido, mulliqué la función aleatoria por 10 y la sume a los datos lineales. El resultado es una mayor dispersión de los puntos, por lo cual la correlación del ajuste lineal disminuyo hasta 0.7859; en estas condiciones este ajuste es muy pobre, incluso se puede pensar en desecharlo.

 

Caso 4. Ahora bien, como tenemos información previa sobre el origen de los datos (como en todo experimento bien planeado), sabemos que el ajuste debe ser lineal, que algunos datos están demasiado alejados de la línea de tendencia; por lo cual, aplicaremos un criterio para eliminar los datos que más se alejan de la línea de tendencia, en este caso el criterio fue tomar a los más alejados a golpe de vista (pues este es un ejemplo didáctico :) ). Esto solo lo puedo hacer si cuento con varios puntos y si confío en el ajuste originalmente elegido. Me quede con 11 datos y obtengo una mejora en el R^2 de 0.7792 a 0.952. Eliminar datos outliers es válido, especialmente si se sistematiza; lo que no es válido es alterar o añadir puntos a conveniencia y sin avisar a quien recibe la información (eso es engañar).

Caso 5. Mejorar la R^2 es solo un criterio para hacer adecuados ajustes de líneas, para nada es una regla increbrantable. Un ejemplo claro es una serie de datos de respuesta que siguen una parábola. Cuando aplicamos una lineal de tendencia obtenemos una R^2 = 0.9435 lo cual es una buena correlación; sin embargo, como sabemos el origen de estos puntos numéricos, es un ajuste equivocado. Lo cual es claro cuando empleando las funciones de Excel ajustamos a una parábola y aumentamos la correlación hasta 1, el valor máximo que se puede obtener.

Conclusión. El factor de correlación entre ajuste de curvas y datos experimentales nos da información sobre lo certero que puede ser el modelo, pero solo es un criterio, que se debe complementar con otra información previa, calculada o inferida.

Actividad sugerida:

Puedes hacer tus propios experimentos numéricos con el archivo original que hice, puedes trabajarlo desde Google Docs. Y recuerda déjanos tus comentarios para mejorar este post que tanta ayuda necesita.

Links de interé:

¿Qué tan bueno es un ajuste? (ingles), para ser más formales sobre el significado de R^2.